1 矩阵的基础

感觉矩阵的题很简单。迅速过完

12.23 一刷

1.1 表示矩阵

在Java中，矩阵通常可以用二维数组（int[][]、double[][]等）来表示。每个内部数组代表矩阵的一行。

int[][] matrix = {
    {1, 2, 3},
    {4, 5, 6},
    {7, 8, 9}
};

1.2 创建矩阵

创建矩阵可以通过直接声明和初始化，或者使用循环动态创建。

int rows = 3;
int columns = 3;
int[][] matrix = new int[rows][columns];
for (int i = 0; i < rows; i++) {
    for (int j = 0; j < columns; j++) {
        matrix[i][j] = i * columns + j;
    }
}

2 36.有效的数独（需要复习）

36. 有效的数独

中等

请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

注意：

一个有效的数独（部分已被填充）不一定是可解的。
只需要根据以上规则，验证已经填入的数字是否有效即可。
空白格用 '.' 表示。

示例 1：

输入：board = 
[["5","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：true

示例 2：

输入：board = 
[["8","3",".",".","7",".",".",".","."]
,["6",".",".","1","9","5",".",".","."]
,[".","9","8",".",".",".",".","6","."]
,["8",".",".",".","6",".",".",".","3"]
,["4",".",".","8",".","3",".",".","1"]
,["7",".",".",".","2",".",".",".","6"]
,[".","6",".",".",".",".","2","8","."]
,[".",".",".","4","1","9",".",".","5"]
,[".",".",".",".","8",".",".","7","9"]]
输出：false
解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

提示：

board.length == 9
board[i].length == 9
board[i][j] 是一位数字（1-9）或者 '.'

分析

题目不难。做的时候没想到的是

没有想到如何判断3*3宫格。（可以用两个坐标来表示9个3*3宫格）

用数组代替hash表存储该行/该列/该3*3宫格是否出现该数字

不用完成数独，但是需要判断给出的数独是否是合法数独。核心思想如下：
1.每行每列每个九宫格均使用一个hash来存储，以此判断该行该列该九宫格是否出现重复数字

具体实现注意以下几点
    （1）可以使用数组代替hash，每行每列都使用一个大小为9*10的二维数组row[9][10] ,col[9][10]来代表hash表，此外，对于九宫格，则使用一个3*3*10维的,subboard[3][3][10]
    row[i][num]:代表第i行出现数字num+1的次数
    col[j][num]:代表第j列出现数字num+1的次数
    subboard[i][j][num]:代表第[i,j]个九宫格中出现数字 num+1的次数
    举个例子，board[i][j]=num,那么，可以用row[i][num-1]++,col[j][num-1]++来表示该行该列出现了数字num
    （2）如何将位置board中的位置映射到对应的九宫格中
    之前纠结于如何判断属于哪个九宫格，认为一共需要9个数来代表9宫格。
看题解后发现可以用两个数来代表九宫格
这样一共九个九宫格可以表述如下
[0,0] [0,1] [0,2]
[1,0] [1,1] [1,2]
[2,0] [2,1] [2,2]
与之对应的，举个例子 [0,0]九宫格中的数的i∈[0,2],j∈[0,2] 
[0,1]:i∈[0,2],j∈[3,5] 
[0,2]:i∈[0,2],j∈[6,8]
可以看到，对于任意坐标(i,j)他会属于[i/3,j/3]九宫格

代码

class Solution {
    public boolean isValidSudoku(char[][] board) {

        //1.初始化数组存储每行每列每个九宫格出现的数字
        int[][] row = new int[9][10];
        int[][] col = new int[9][10];
        int[][][] subboard = new int[3][3][10];

        //2.遍历board中的每个元素
        for(int i = 0;i<9;i++){
            for(int j = 0;j<9;j++){
                if(board[i][j]=='.')continue;
                //2.1 遍历时，将该元素加入1中初始化的数组中，判断结果是否>1,是的话直接返回false
                int num = board[i][j]-'0';
                row[i][num-1]++;
                col[j][num-1]++;
                subboard[i/3][j/3][num-1]++;
                if(row[i][num-1]>1 || col[j][num-1]>1 || subboard[i/3][j/3][num-1]>1){
                    return false;
                }
            }
        }
        return true;
        

    }

}

3 54.螺旋矩阵（需要复习）

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

1 2	输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[1,2,3,6,9,8,7,4,5]

示例 2：

1 2	输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] 输出：[1,2,3,4,8,12,11,10,9,5,6,7]

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 10
-100 <= matrix[i][j] <= 100

分析

之前做过很多次。但是再做仍然会出现问题。具体是一些细节上的问题。

这次做能够知道3，4需要判断当前行是否遍历过，当前列是否遍历过

但是没有注意到的点为
举个例子，往右的时候需要初始化当前列，即j=left。就是在往一个方向遍历移动的时候，需要初始化最开始移动的那个下标。

第一次做的时候，里面的移动用的是for循环，而不是while，所以使用while来遍历的话，就需要在遍历的一开始指定j
1
2
3
4
5
6
7
j = left;
while(j<right){
    res.add(matrix[top][j]);
    j++;
    num++;
}
top++;

模拟。
用四个指针作为边界，分别为top，bottom，left，right作为上下左右的边界[top,bottom),[left,right)
i，j则指向当前元素

具体而言
1.j<right的时候，往右，到右边界时，top++,往下
2.i<bottom的时候，往下，到下边界时，right--,往左
3.j>=left的时候，往左，到左边界时，bottom--,往上。
4.i>=top的时候，往上，到上边界时，left++,继续重复1-4的步骤

注意，3，4要判断一下，对于3要判断当前行是否遍历过，即判断top<bottom,对于4的话则是判断left<right,满足的话才往左往上遍历

代码

class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        /**

         */
        int top = 0,bottom = matrix.length,left=0,right=matrix[0].length;
        int num=0;
        int i=0,j=0;
        List<Integer> res = new ArrayList<>();
        while(num<matrix.length*matrix[0].length){
            j = left;
            while(j<right){
                res.add(matrix[top][j]);
                j++;
                num++;
            }
            top++;

            i=top;
            while(i<bottom){
                res.add(matrix[i][right-1]);
                i++;
                num++;
            }
            right--;

            j=right-1;
            while(top<bottom && j>=left){
                res.add(matrix[bottom-1][j]);
                j--;
                num++;
            }
            bottom--;

            i=bottom-1;
            while(left<right && i>=top){
                res.add(matrix[i][left]);
                i--;
                num++;
            }
            left++;
        }
        return res;
    }
}

4 48.旋转图像

48. 旋转图像

中等

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在** 原地** 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

1 2	输入：matrix = [[1,2,3],[4,5,6],[7,8,9]] 输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

1 2	输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] 输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

提示：

n == matrix.length == matrix[i].length
1 <= n <= 20
-1000 <= matrix[i][j] <= 1000

思路

没什么好说的，一遍过。

做过之后就是挺简单的题目

1
2
3

容易证明
先上下翻转
之后按照从左上->右下的对角线反转，即为结果

代码

class Solution {
    public void rotate(int[][] matrix) {
        /**

         */
        //1.先上下翻转,matrix[i][j] <->matrix[n-i-1][j]
        int n = matrix.length;
        for(int i = 0;i<n/2;i++){
            for(int j = 0;j<n;j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n-i-1][j];
                matrix[n-i-1][j] = temp;
            }
        }

        //2.按照对角线翻转matrix[i][j] <-> matrix[j][i]
        for(int i = 0;i<n;i++){
            for(int j = 0;j<i;j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        return;
    }
}

5 73.矩阵置零（一遍过）

73. 矩阵置零

中等

给定一个 *m* x *n* 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用原地算法。

示例 1：

1 2	输入：matrix = [[1,1,1],[1,0,1],[1,1,1]] 输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

1 2	输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] 输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

m == matrix.length
n == matrix[0].length
1 <= m, n <= 200
-231 <= matrix[i][j] <= 231 - 1

进阶：

一个直观的解决方案是使用 O(*m**n*) 的额外空间，但这并不是一个好的解决方案。
一个简单的改进方案是使用 O(*m* + *n*) 的额外空间，但这仍然不是最好的解决方案。
你能想出一个仅使用常量空间的解决方案吗？

5.1 思路

用了标记数组。

两个数组标记
row[m]:row[i]标记第i行是否出现0
col[n]:col[j]标记第j行是否出现0

1.遍历matrix数字，为row和col两个标记数组赋值，从而得到 每行/每列是否出现0 的结果
2.根据row和col两个数组，为原数组赋值

5.2 代码

class Solution {
    public void setZeroes(int[][] matrix) {
        /**

         */
        int m = matrix.length;
        int n = matrix[0].length;
        int[] row = new int[m];
        int[] col = new int[n];

        for(int i=0;i<m;i++){
            for(int j = 0;j<n;j++){
                if(matrix[i][j]==0){
                    row[i]=1;
                    col[j]=1;
                }
            }
        }

        for(int i = 0;i<m;i++){
            if(row[i]==1){
                for(int j = 0;j<n;j++){
                    matrix[i][j]=0;
                }
            }
        }

        for(int j = 0;j<n;j++){
            if(col[j]==1){
                for(int i=0;i<m;i++){
                    matrix[i][j]=0;
                }
            }
        }
        return;
    }
}

6 289.生命游戏（一遍过）

289. 生命游戏

中等

根据百度百科， 生命游戏 ，简称为生命，是英国数学家约翰·何顿·康威在 1970 年发明的细胞自动机。

给定一个包含 m × n 个格子的面板，每一个格子都可以看成是一个细胞。每个细胞都具有一个初始状态： 1 即为 活细胞 （live），或 0 即为 死细胞 （dead）。每个细胞与其八个相邻位置（水平，垂直，对角线）的细胞都遵循以下四条生存定律：

如果活细胞周围八个位置的活细胞数少于两个，则该位置活细胞死亡；
如果活细胞周围八个位置有两个或三个活细胞，则该位置活细胞仍然存活；
如果活细胞周围八个位置有超过三个活细胞，则该位置活细胞死亡；
如果死细胞周围正好有三个活细胞，则该位置死细胞复活；

下一个状态是通过将上述规则同时应用于当前状态下的每个细胞所形成的，其中细胞的出生和死亡是同时发生的。给你 m x n 网格面板 board 的当前状态，返回下一个状态。

给定当前 board 的状态，更新 board 到下一个状态。

注意你不需要返回任何东西。

示例 1：

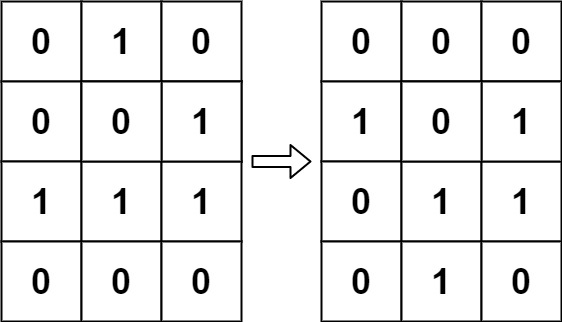
1 2	输入：board = [[0,1,0],[0,0,1],[1,1,1],[0,0,0]] 输出：[[0,0,0],[1,0,1],[0,1,1],[0,1,0]]

示例 2：

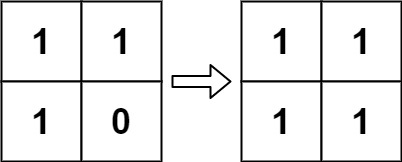
1 2	输入：board = [[1,1],[1,0]] 输出：[[1,1],[1,1]]

提示：

m == board.length
n == board[i].length
1 <= m, n <= 25
board[i][j] 为 0 或 1

进阶：

你可以使用原地算法解决本题吗？请注意，面板上所有格子需要同时被更新：你不能先更新某些格子，然后使用它们的更新后的值再更新其他格子。
本题中，我们使用二维数组来表示面板。原则上，面板是无限的，但当活细胞侵占了面板边界时会造成问题。你将如何解决这些问题？

分析

之前做过有印象。

只要能明白下面的东西就好做了。
    活->死 的细胞，用-1表示
    死->活 的细胞，用-2表示

总结一下规则
活细胞：当且仅当周围8个位置只有2/3个活细胞的时候，才能活
死细胞：当周围8个位置正好有3个活细胞的时候，才能复活

假如要原地算法的话，我们在更新细胞的时候，会发现还存在两种状态，即原本是活细胞，现在死了，原本是死细胞，现在活了。这两个状态我们用另外两个数来代表
活->死 的细胞，用-1表示
死->活 的细胞，用-2表示

那么，在第一遍遍历的时候，
对活细胞，该细胞周围 状态绝对值为1的细胞个数为2，3 ，该细胞仍然活着，不更改装填
        否则，将该细胞状态从1置为-1
对死细胞，该细胞周围 状态绝对值为1的细胞个数为3，该细胞死而复生，状态修改为-2

第二遍遍历，根据-1和-2修改对用的值，-1状态的修改为0，因为死了已经。
-2状态的修改为1，因为死细胞活了

代码

class Solution {
    public void gameOfLife(int[][] board) {
        /**

         */
        int m = board.length;
        int n = board[0].length;

        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                int num = getLifeNum(board,i,j);
                if(board[i][j]==1 && num!=2 && num!=3){
                    board[i][j]=-1;
                }else if (board[i][j]==0 && num==3){
                    board[i][j]=-2;
                }
            }
        }

        for(int i = 0;i<m;i++){
            for(int j = 0;j<n;j++){
                if(board[i][j]==-1){
                    board[i][j]=0;
                }else if(board[i][j]==-2){
                    board[i][j]=1;
                }
            }
        }
        return;
    }

    public int getLifeNum(int[][] board,int x,int y){
        int m = board.length;
        int n = board[0].length;
        int num=0;
        int[][] dirc = {{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}};
        for(int i = 0;i<8;i++){
            if(x+dirc[i][0]>=0 && x+dirc[i][0]<m && y+dirc[i][1]>=0 && y+dirc[i][1]<n && Math.abs(board[x+dirc[i][0]][y+dirc[i][1]])==1){
                num++;
            }
        }
        return num;
    }
}

【LeetCode 面试经典150题】4-矩阵

1 矩阵的基础

1.1 表示矩阵

1.2 创建矩阵

相关题目

2 36.有效的数独（需要复习）

分析

代码

3 54.螺旋矩阵（需要复习）

分析

代码

4 48.旋转图像

思路

代码

5 73.矩阵置零（一遍过）

5.1 思路

5.2 代码

6 289.生命游戏（一遍过）

分析

代码

1 矩阵的基础

1.1 表示矩阵

1.2 创建矩阵

相关题目

2 36.有效的数独 （需要复习）

分析

代码

3 54.螺旋矩阵（需要复习）

分析

代码

4 48.旋转图像

思路

代码

5 73.矩阵置零 （一遍过）

5.1 思路

5.2 代码

6 289.生命游戏 （一遍过）

分析

代码

2 36.有效的数独（需要复习）

5 73.矩阵置零（一遍过）

6 289.生命游戏（一遍过）